Turunan Fungsi Aljabar
Pengertian Turunan Fungsi Aljabar
Turunan fungsi aljabar adalah fungsi baru hasil penurunan pangkat dari fungsi sebelumnya menurut aturan yang telah ditetapkan. Jika diimplementasikan di dalam grafik fungsi, turunan ini merupakan gradien garis singgung terhadap grafik di titik tertentu. Tingkat turunan fungsi tidak terbatas pada satu tingkat saja, tetapi juga bisa dua tingkat, tiga tingkat, dan seterusnya. Konsep turunan setiap tingkatnya juga sama. Hanya saja, fungsi yang diturunkan berbeda-beda karena mengacu pada hasil turunan sebelumnya.
Konsep Turunan Fungsi Aljabar
Pada dasarnya, turunan fungsi aljabar merupakan bentuk lain dari suatu limit fungsi yang nilainya mendekati nol. Misalnya saja, seseorang berkendara menggunakan motor dengan kecepatan 60 km/jam. Saat berkendara, apakah orang tersebut bisa mengondisikan untuk tetap berada di kecepatan itu? Tentu tidak, kan? Lalu, apa artinya 60 km/jam? Kecepatan tersebut merupakan kecepatan rata-rata. Secara matematis, dirumuskan sebagai berikut.
posisi orang tersebut (s) selalu berubah setiap waktu (t). Artinya, posisi bisa dinyatakan sebagai fungsi waktu (s2 = f(t) ). Nah, t2 merupakan waktu setelah bergerak selama h atau t2 = t1 + h. Jika disubstitusikan ke persamaan kecepatan rata-rata menjadi:Untuk nilai h yang sangat kecil, h bisa dinyatakan mendekati nol (h → 0). Apa artinya? Jika nilai h mendekati nol, akan berlaku fungsi kecepatan sesaat seperti berikut
Persamaan di atas merupakan bentuk laju perubahan jarak terhadap waktu atau turunan fungsi jarak terhadap waktu.
Jika diterapkan pada sembarang f(x), akan berlaku laju perubahan f(x) terhadap x atau turunan pertama f(x) terhadap x (f’(x)), sehingga persamaannya menjadi:
Rumus Turunan Fungsi Aljabar
Persamaan turunan yang memuat fungsi limit efektif digunakan untuk persamaan fungsi linear atau pangkat 1. Namun, rumus tersebut kurang efektif jika digunakan pada persamaan fungsi aljabar yang derajat polinomnya lebih dari 1 (pangkat lebih dari 1). Untuk itu, kamu bisa menggunakan rumus-rumus berikut.
1. f(x) = b → f’(x) = 0
Suatu konstanta akan bernilai nol jika diturunkan, contoh f(x) = 15 → f’(x) = 0.
2. f(x) = bx → f’(x) = b
Jika variabel x diturunkan terhadap x, akan menghasilkan 1. Contoh:
- f(x) = x → f’(x) = 1
- f(x) = 2x → f’(x) = 2
- f(x) = 5x – 3 →f’(x) = 5
- f(x) = axn → f’(x) = naxn-1
Rumus di atas berlaku untuk turunan fungsi pangkat, ya. Saat menurunkan suatu fungsi, artinya kamu sedang mencari turunan pangkat dari fungsi tersebut atau pangkatnya menjadi lebih kecil. Misal, jika variabel x2 diturunkan terhadap x, maka derajat variabelnya akan berkurang 1 menjadi x. Jika variabel x3 diturunkan terhadap x, maka derajat variabelnya akan berkurang 1 menjadi x2 dan seterusnya. Perhatikan contoh berikut.
f(x) = 6x4 + 2x3 → f’(x) = (4)(6)x3 + (3)(2)x2 = 24x3 + 6x2
Turunan fungsi aljabar juga bisa dinyatakan dalam bentuk notasi Leibniz seperti berikut.
Pengertian Persamaan Garis Singgung
Persamaan garis singgung adalah persamaan garis yang menyinggung lingkaran di satu titik. Suatu garis disebut garis singgung jika memiliki tepat satu titik persekutuan atau titik potong terhadap lingkaran atau kurva. Lalu, apa perbedaan garis singgung lingkaran dan kurva? Perbedaannya terletak pada objek yang disinggung. Jika suatu garis menyinggung lingkaran, maka garis singgungnya disebut garis singgung lingkaran. Sebaliknya, jika yang disinggung berupa kurva, maka garis singgungnya disebut garis singgung kurva. Perhatikan contoh
Persamaan Garis Singgung Lingkaran
Dengan adanya garis singgung, dihasilkan suatu titik yang disebut titik singgung. Titik singgung merupakan titik potong antara garis singgung dan jari-jari lingkaran. Dari titik singgung itu, kamu bisa menentukan persamaan garis singgungnya. Berdasarkan titik yang dilaluinya, persamaan garis singgung lingkaran bisa dicari dengan tiga cara, yaitu sebagai berikut.
Persamaan Garis Singgung yang Melalui Satu Titik pada Lingkaran
Jika suatu garis menyinggung lingkaran yang berpusat di titik (0,0) tepat di titik A(x1, y1), maka persamaan umum garis singgungnya bisa dinyatakan sebagai berikut.
Dengan:
m = gradien garis singgung;
y1 = koordinat titik potong sumbu-y; dan
x1 = koordinat titik potong sumbu-x.
Oleh karena garis singgung lingkaran selalu tegak lurus dengan jari-jari lingkaran, maka hasil kali gradien garis singgung dan gradien jari-jari selalu (-1). Dengan demikian:
Jika gradien tersebut disubstitusikan ke persamaan umum garis singgung lingkarn, diperolehPersamaan (1) itulah yang nantinya bisa kamu gunakan untuk menentukan persamaan garis singgung lingkaran di titik A(x1, y1) dengan titik pusat (0, 0).Contoh Soal
Mula-mula, kamu harus memastikan titik singgung (3, 4) berada pada lingkarannya. Caranya, substitusikan koordinat titik A(3, 4) ke persamaan lingkaran x2 + y2 = 25. Jika hasilnya sama dengan 25, maka koordinat itu merupakan benar titik singgungnya.
Setelah kamu memastikan kebenaran titik singgungnya, selanjutnya, substitusikan koordinat titik A(3, 4) ke persamaan garis singgung pada persamaan (1)
Jadi, persamaan garis singgungnya adalah 3x + 4y – 25 = 0. Adapun bentuk penggambaran garis singgung lingkarannya adalah seperti berikut.
Uji Turunan Kedua
Sebagai tambahan untuk menguji kecekungan, turunan kedua dapat digunakan untuk untuk melakukan pengujian terhadap maksimum dan minimum lokal. Pengujian ini berdasarkan fakta bahwa jika suatu grafik fungsi f cekung ke atas pada selang buka yang memuat c, dan f ’(c) = 0, maka f(c) haruslah minimum lokal f. Demikian juga, jika grafik suatu fungsi f cekung ke bawah pada selang buka yang memuat c, dan f ’(c) = 0, maka f(c) haruslah maksimum lokal f. Perhatikan gambar di bawah ini.
Teorema Uji Turunan Kedua
Misalkan f fungsi kontinu sedemikian sehingga f ’(c) = 0 dan turunan keduanya ada pada selang buka yang memuat c.
- Jika f ”(c) > 0, maka f memiliki minimum lokal pada (c, f(c)).
- Jika f ”(c) < 0, maka f memiliki maksimum lokal pada (c, f(c)).
Jika f ”(c) = 0, maka pengujiannya gagal, atau dengan kata lain, f mungkin memiliki maksimum lokal, minimum lokal, atau tidak memiliki keduannya. Pada kasus ini, kita harus menggunakan Uji Turunan Pertama.
Pembuktian
Jika f ’(c) = 0 dan f ”(c) > 0, maka ada selang buka I yang memuat c sedemikian sehingga
untuk semua x ≠ c dalam I. Jika x < c, maka f ’(x) < 0. Demikian juga, jika x > c, maka x – c > 0 dan f ’(x) > 0. Jadi, f ’(x) berubah dari negatif menjadi positif pada c, dan berdasarkan Uji Turunan Pertama, f(c) merupakan minimum lokal f. Pembuktian kasus kedua serupa dengan pembuktian kasus pertama tersebut.



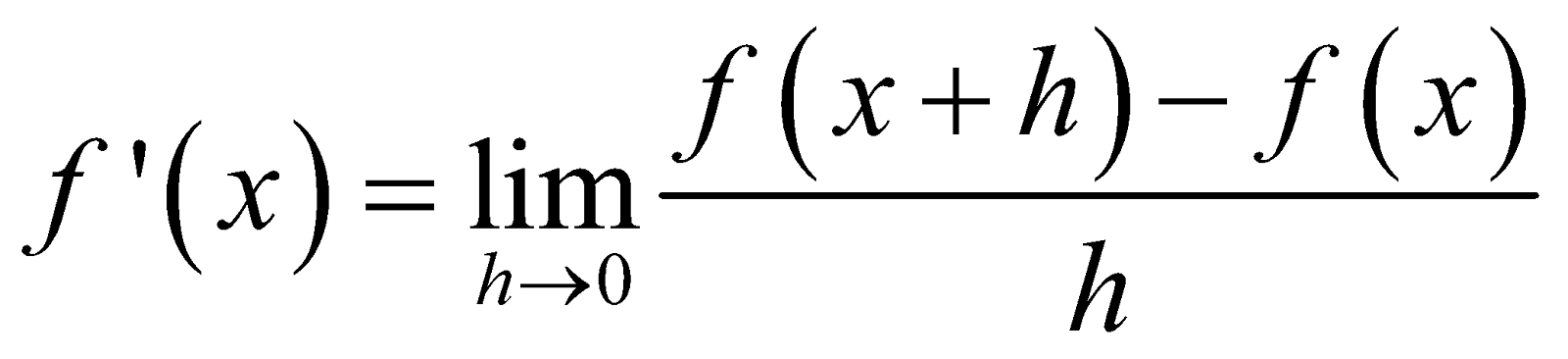




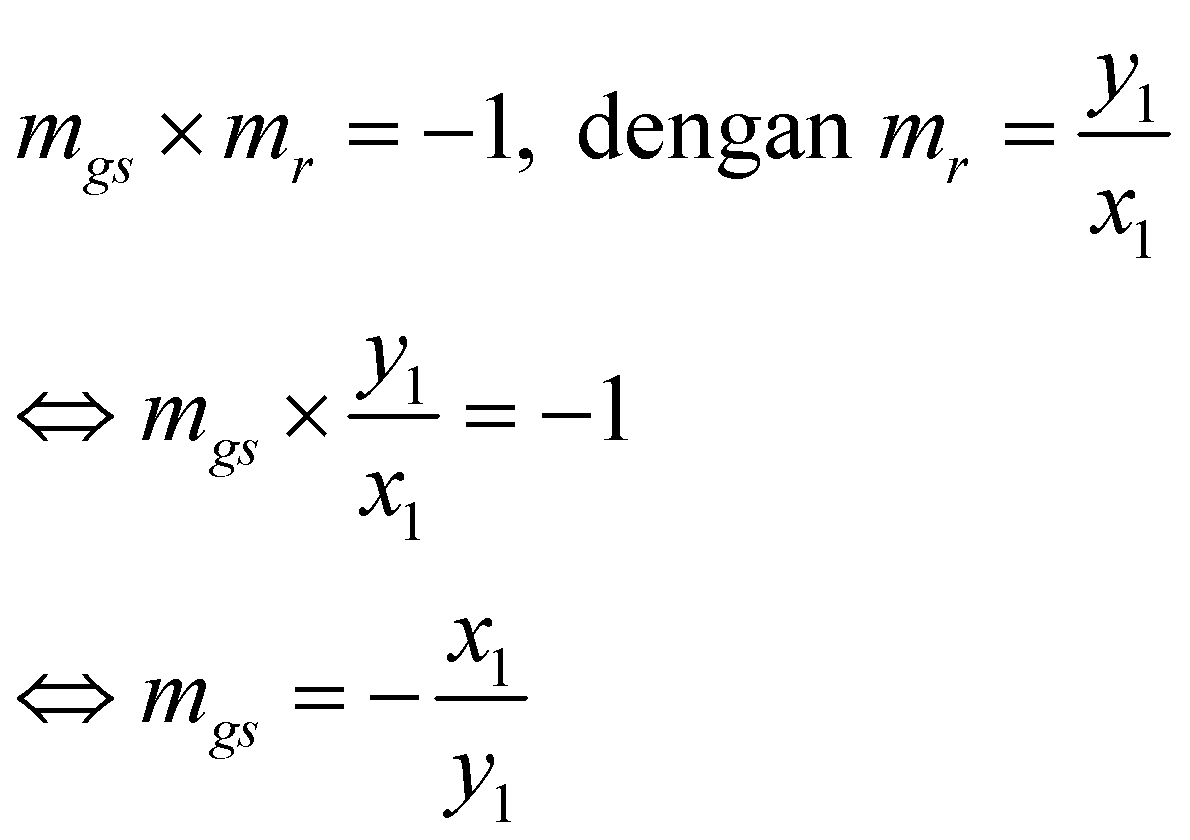


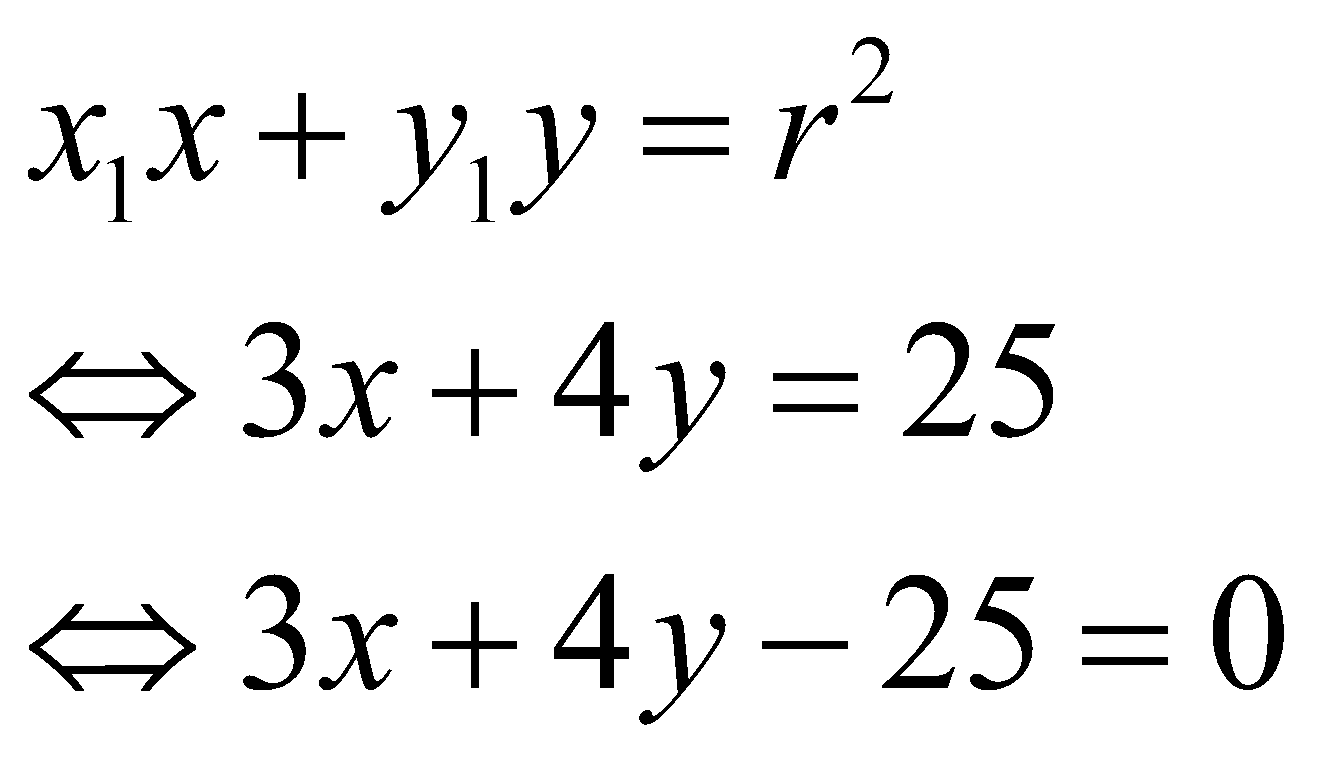




Comments
Post a Comment